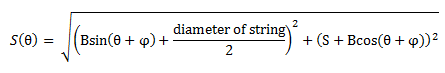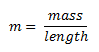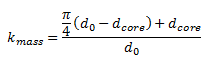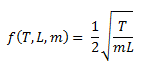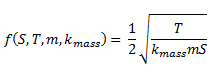Quantitative Analysis of the Musicality of an Electric Guitar Tremolo
From DDL Wiki
Contents |
Mechanical Analysis
Summary of Quantitative Analysis
In our quantitative analysis, we chose to analyze the forces acting upon the bridge. As an offshoot of this, we were also able to analyze the effect of using the bridge on the pitch of the strings. We determined that although each of the components of the guitar bridge act in an easily predictable linear fashion, the complex combination of all the factors combine together into a very non-linear system. The main independent variable of our device is the angle that the bridge is depressed by the guitarist. We called this variable theta.
For our analysis, we used a simplified, but relatively accurate model of the guitar bridge. The Floyd Rose bridge is functionally very similar to our bridge model. The original Fender bridge has a number of design flaws which introduce large unpredictable changes to the forces on the strings, which we could not model easily. Consider our model a “best case scenario” for a pivoting bridge. Any tuning problems with our model would be exacerbated, not alleviated in a real world implementation.
Assumptions
1. The strings are fixed at both the bridge and the nut. Without this assumption, the unpredictable shifting of the strings at the tuners and ball-ends introduces additional tuning problems. The Floyd Rose bridge employ’s clamps at the bridge and nut which fix the strings.
2. Strings behave as steel linear springs. Strings are made of nickel steel alloys. Since the exact recipe for the steel is a closely guarded industry secret, we assumed the properties of the strings match that of standard stainless steel. The density of stainless steel is 7800 kg/m3 and the elastic modulus is 200 GPa.
3. The guitar neck and body do not deform. In a real guitar, the body and neck are made of wood, and deform under the tension of the strings. This deformation is very small, and we chose to ignore it for simplicity.
4. Small Angle Assumption. We meant this not in the trigonometric sense (sin(angle) = angle, and cos(angle) = 1), but in the sense that the bridge is only meant to function at relatively small values of theta. We assumed a maximum angle of 12 degrees. Beyond this angle, the the strings are all completely limp, and at some point, the bridge would break.
5. We assumed that the strings used are of the common “8-42” variety. The string diameters are 8, 11, 15, 22, 30, and 42 thousandths of an inch. The thickest three strings are thinner steel cores wrapped with wire, which provide increased linear mass without making the strings too stiff to vibrate.
| String | Diameter (inches) | Diameter (m) | Core Area (m^2) | Tension (N) | Pressure (Pa) | Deflection (mm) | Standard Tuning (Hz) | Linear Mass (kg/m) |
|---|---|---|---|---|---|---|---|---|
| e | 0.009 | 0.000229 | 4.10e-8 | 46.1 | 1.13e9 | 5.63 | 329.6 | 0.0001673 |
| B | 0.011 | 0.000279 | 6.13e-8 | 49.0 | 7.99e8 | 3.99 | 246.9 | 0.0003163 |
| G | 0.016 | 0.000406 | 12.97e-8 | 57.4 | 4.42e8 | 2.21 | 196 | 0.000588072 |
| D | 0.024 | 0.000330 | 8.56e-8 | 59.3 | 6.93e8 | 3.46 | 146.8 | 0.001084068 |
| A | 0.032 | 0.000381 | 11.40e-8 | 62.5 | 5.48e8 | 2.74 | 110 | 0.002033498 |
| E | 0.042 | 0.000406 | 12.97e-8 | 65.7 | .07e8 | 2.53 | 82.4 | 0.003809595 |
Table 1: Properties Assumed (or calculated) of Guitar Strings
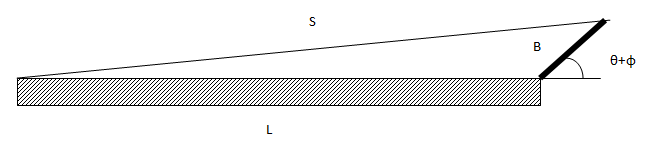
Figure 1: The Simplified Guitar Model Used for Analysis
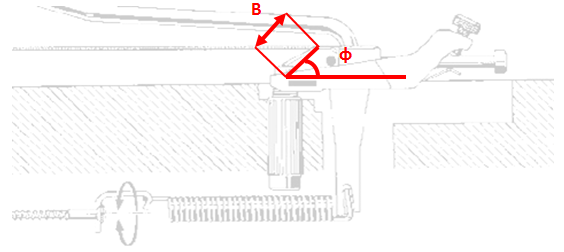
Figure 2: Close Up of Guitar Bridge with Assumptions for Analysis
| Symbol | Definition | Value |
|---|---|---|
| L | Length fo the guitar scale, from the nut to the bridge pivot. | 25 inches, or 0.635 meters |
| B | The length of hte bridge from the pivot point to the point where the strings make contact with the bridge. | 3/8 of an inch, or 0.01346962 meters |
| S | The length of the string. | Variable function (function of θ) |
| φ | The "at rest" angle of the bridge | 45 degrees |
| θ | The additional, user supplied angle to the bridge. | Independent variable |
Table 2: Variable Definitions
Determining the String Tension
Each string on the guitar is made out of a very thin wire of nickel steel. The wire is either made of solid steel, or a solid steel core wrapped in another coil of steel wire. This wrapping allows the string to have a relatively high mass, while remaining flexible, as a solid string of the same thickness would be very hard to pluck. The wires can be viewed as springs, since under standard guitar tuning, the strings stretch an appreciable amount. Although each string can be viewed as an ideal spring, the combination of the tension forces of all six strings on the bridge is a non-linear function when compared to the angle of the tremolo.
One cause of this non-linearity is the fact that for any string, its tension vs. bridge angle function is a piecewise function. The tension in the string decreases linearly as the bridge angle increases, but when the tension reaches zero, the string does not compress like an ideal spring would. Instead, the tension remains zero. When you add together all six string functions, the resulting total plots as a curve, not a straight line.
Derivation
The strings behave as springs. Therefore, we will use Hooke’s spring law to determine the tension.
Where F is the spring force, k is the spring constant, and x is the stretch or compression of the spring. To determine the force of a spring in preexisting tension, we can add a constant to the format:
Substituting the appropriate variables for the guitar problem gives us this equation.
T0 is the tension of the guitar strings in standard tuning.
kstring is the string constant of the string.
S(0) is the neutral length of the string.
S(θ) is the length of the strings when the bridge is at angle θ.
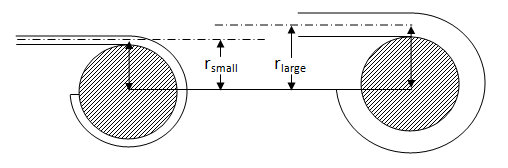
Further deviation from the expected linear result is caused by effect of the string diameter on the rotation of the bridge. The bridge can be idealized as a pulley, around which the string is wrapped. When the pulley turns, the string is wound or unwound. Each string is not infinitely thin, so the radius of the pulley is different for each string. Therefore, the uniform rotation of the bridge allows a different amount of additional slack for each string.
Figure 4: String Radius's Effect on Tuning
Forces and Moments
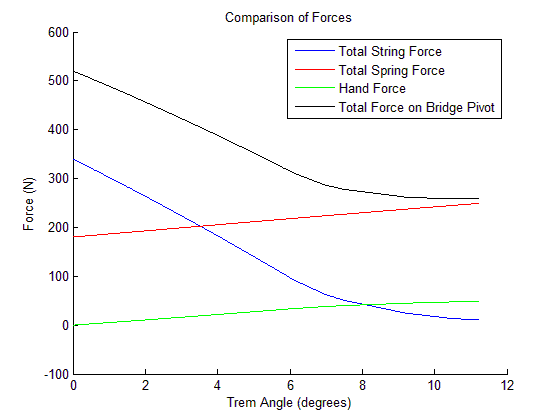
Overall, the predictions of our mathematical model match very closely our hands on experience with the guitar bridge. The mathematical model predicts a force of around 10 pounds to depress the bridge appreciably, which the mathematical model backs up. This force seems to be an appropriate amount for ease of use, as too little force would allow the bridge to detune by accident, and too much force would make it too difficult to use. All the members of our group (guitarists and non-guitarists alike) felt that the amount of force required to operate the bridge was appropriate. The forces in the springs, which serve to create a counter-force to that of the strings, was lower than we expected, being less than ½ the force of the strings when the bridge is in its neutral position. When dissecting the guitar, we found removal of these springs to be quite difficult, and originally attributed it to high tension in the springs. This initial impression seems to be incorrect, as each spring is under only 15 lbs of tension. The bridge pivot serves as the mounting point and pivot for the guitar bridge. As such, it is the location where large forces are most likely. This proved correct in our mathematical analysis. In its neutral position, the pivot had to provide 500 N of force, or almost 120lb. The area over which this force is provided is very small (a few square millimeters), meaning that the pressure there is astronomically high. Distributing this pressure would be a possible direction for this project to take, as the pivot point of the bridge is a frequent point of wear and breakage on guitars.
Derivation
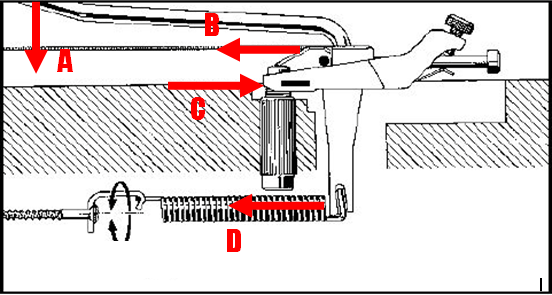
Figure 6: Diagram of Bridge with Forces
Image from http://www.jemsite.com/tech/1setup.htm#step1 , taken from Ibanez Guitar Setup Booklet
| Variable | Description |
|---|---|
| A | Hand Force (User pushing on the lever) |
| B | String Tension |
| C | Pivot Force (at the mounting point) |
| D | Spring Tension |
Table 3: Force Definitions
The sum of the forces on the bridge can be expressed as such:
The sum of the moments on the bridge, summed around the pivot point, is as follows:
Where hbridge is 1”, lhandle is 5 ¾”, measured from the guitar.
String Frequency
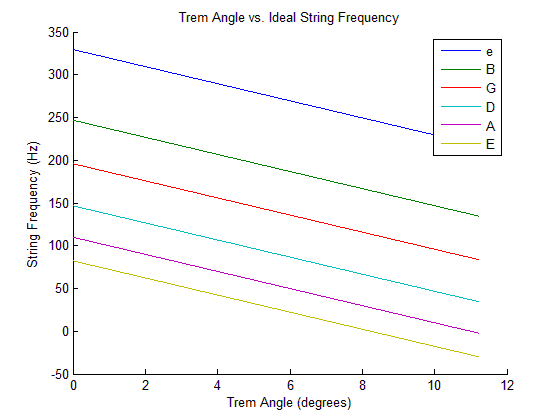
An ideal guitar bridge would allow a guitarist to detune his guitar musically. This would mean that each string’s fundamental frequency would retain a linear relationship with the other strings. Such a bridge would have a frequency vs. bridge rotation graph similar to this one:
Figure 7: Ideal Angle vs. Frequency Graph
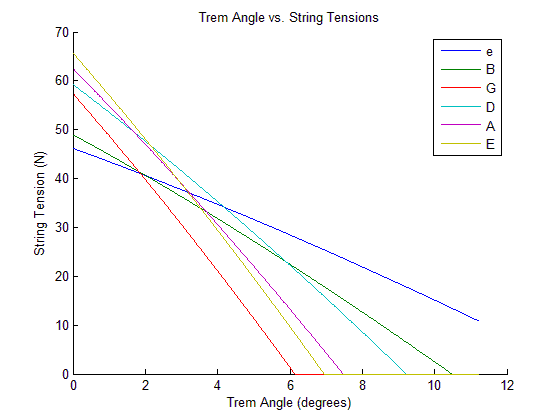
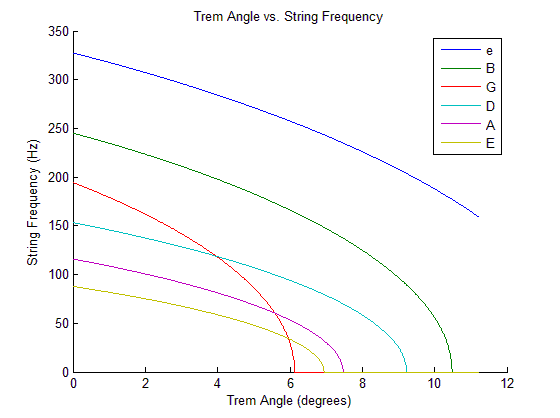
Using our mathematical model, we calculated the response of an actual guitar bridge, which looks like this:
Figure 8: Actual Angle vs. Frequency Graph
This graph shows that not only do the strings not behave linearly, but they also do not maintain a linear relationship to each other. This effect is especially noticeable on the G string of the guitar, which detunes much faster than the other strings. In practical terms, this means that the guitarist is not able to play chords when using the tremolo bridge of the guitar, as the strings no longer are in the same tune, so playing two of them together will sound dissonant. This limits the guitarist to only using the tremolo bridge for playing single notes, or chaotic dissonant noises. Being able to play chords and detune them musically would open up many musical possibilities currently not available to guitarists.
Derivation
In order to determine the frequency of the string, we need to know the length of the string as a function of the position of the bridge.
The length of the string is actually a use of the Pythagorean theorem, as can be seen in the illustration of our guitar model, the string is the hypotenuse of a triangle with sides formed by the guitar body, and the bridge. The height of the triangle is a function of the sine of angle of the bridge, and the thickness of the string. The length of the triangle is the sum of the length of the body, and the cosine of the angle of the bridge. We need to determine the linear mass of the string. The linear mass is the mass per length of string.
For the solid strings, this is easy to determine. For the wound strings, the linear mass is harder to determine. I used this formula, found at http://terrydownsmusic.com/technotes/StringGauges/STRINGS.HTM to determine the corrective coefficient to get the correct linear mass.
Where d0 is the total diameter of the string, and dcore is the diameter of the solid metal core.
The equation for a vibrating string is as follows:
Substituting the correct variables for the guitar example, the frequency of the string is a function of the length of the string, the tension, the linear mass, and where necessary, the corrective coefficient for linear mass. Note that for solid strings, the corrective coefficient is equal to 1.
Since S and T are actually functions of θ, the equation for frequency can be written in this form:
Using the equation and the string properties from Table 1, we were able to create the graph seen above.
Conclusion
Through our analysis, we discovered several things that will be useful to our future task redesigning the guitar bridge.
Firstly, the musicality of the strings when the bridge is used is not very good. The strings to not stay in tune relative to each other at all. This is not a small problem, but a fundamental issue with the current "rotational" tremolo design.
Secondly, the force required by the user to activate the bridge is about 50 N maximum. This is a very reasonable number, and should be our goal for any alternative designs we consider. The force of the springs on the bridge is similarly reasonable, and is not a design problem. The only force that is worryingly large is the force at the pivot points. Since this force is concentrated into a very small area, it has the potential to fatigue the metal very quickly. We might chose to design a bridge with a larger contact area for this force, which would improve the reliability of the bridge.