Downhill simplex
From DDL Wiki
(→'''Types of Moves''') |
(→'''Simplex''') |
||
| Line 4: | Line 4: | ||
== '''Simplex''' == | == '''Simplex''' == | ||
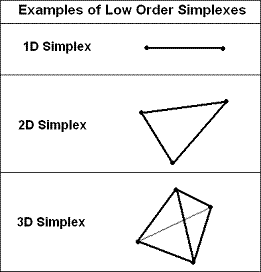
| - | The method revolves around a simplex; a geometric object which contains n+1 vertices where n is the number of independent variables. For instance, in the case of a one dimensional optimization the simplex would contain two points and represent a line segment. In a two dimensional optimization, a three pointed triangle would be used. | + | The method revolves around a simplex; a geometric object which contains n+1 vertices where n is the number of independent variables. For instance, in the case of a one dimensional optimization the simplex would contain two points and represent a line segment. In a two dimensional optimization, a three pointed triangle would be used (Figure 1). |
| + | |||
| + | [[Image:004.gif]] | ||
| + | Figure 1: | ||
| - | |||
== '''Comparison''' == | == '''Comparison''' == | ||
Revision as of 13:26, 11 January 2007
The Downhill Simplex method is a multidimensional optimization method which uses geometric relationships to aid in finding function minimums. One distinct advantage of this method is that it does not require taking the derivative of the function being evaluated. Instead it creates its own pseudo-derivative by evaluating enough points to define a derivative for each independent variable of the function.
Contents |
Simplex
The method revolves around a simplex; a geometric object which contains n+1 vertices where n is the number of independent variables. For instance, in the case of a one dimensional optimization the simplex would contain two points and represent a line segment. In a two dimensional optimization, a three pointed triangle would be used (Figure 1).
Comparison
Each vertex of the simplex will have a function value, and the points with lower values are obviously superior. By evaluating each point the algorithm is creating pseudo-derivatives of the function at the location of the simplex. The definition of a derivative is: [[latex($$ \frac{lim}{x->0} \frac{f(x+h)-f(x)}{h} $$)]]
In this case the values of h for each derivative do not approach zero but instead are equal to the distance between the two points. This is, however, enough information for the method to choose which direction produces better values. The goal of the function is then to move the simplex away from points of high value.
Moving
The downhill simplex method can employ several methods for moving the simplex downhill. These methods include reflection, reflection with expansion or contraction, contraction, and shrinkage. For each iteration, the method chosen depends on both data known from the current simplex location as well as data from previous moves.
Types of Moves
Reflection
During a reflection, the point of highest value is reflected to the opposite side of the simplex. By doing this the vertex of highest value is replaced by a point that occurs in the direction of the steepest gradient. This is an efficient way for the simplex to move toward lower values.
Reflection and Expansion/Contraction
In order to make reflections more efficient, the magnitude of each reflection may be weighted. These weights may be used to increase the effective step size so that less iteration are necessary to cover a given distance. In addition to controlling step size, utilizing expansion and contraction may also be used to control the directionality and orthogonality of the simplex. This way, if the function appears to have a very steep slope in one direction but not another, it may travel quickly down that slope. Likewise, if the function is in an area of rapidly changing slopes, the algorithm can make a small change which will allow for greater precision between steps.
Contraction
There are cases when an minimum has not been found, but all superior points are within the volume of the simplex. In these cases it is undesirable to move the simplex (as this will produce less larger results) yet some sort of change is necessary for improvement. In cases like this, the best approach may be to reduce the size of the simplex. With the method of contraction, the point of highest value is replaced by a point which is closer to the other vertices of the simplex. Doing this not only allows the simplex to evaluate points which are currently within its volume, but also allows for finer resolution. This method of is generally only useful once the simplex is very close to the optimum.
Shrinkage
Instead of contracting only one vertex, multiple vertices may be contracted in one iteration. This is referred to as shrinkage and is a faster method for reducing the size of the simplex. With this method the vertex of lowest value remains fixed and all other points are moved toward that location.
Optimization Examples
References