Multi-Objective Optimization

From DDL Wiki

Revision as of 12:34, 11 January 2007

Introduction

When an optimization problem involves more than one objective function, the task of finding one or more optimum solutions is known as Multi-Objective Optimization. Most real-world search and optimization problems naturally involve multiple objectives. Diffrenet solutions may produce trade-offs (conflicting scenarios) among different objectives. A solution that is extreme (in a better sense) with respect to one objective requires a compromise in other objectives. This prohibits one to choose a solution which is optimal with respect to only one objective.

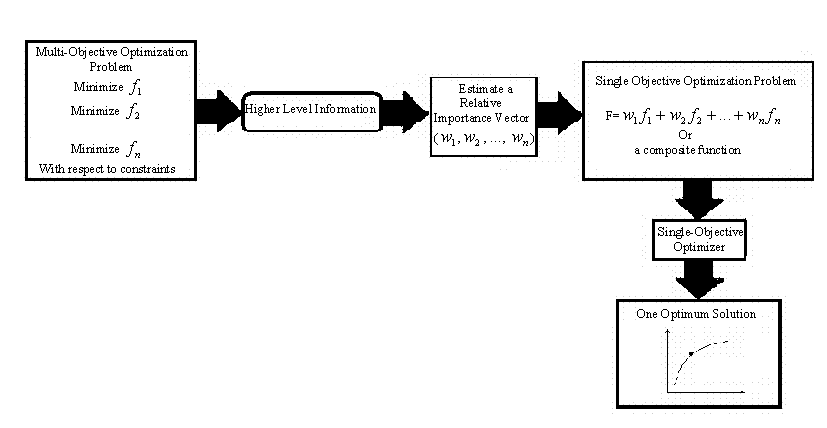
As in case of single-objective optimization, multi-objective optimization has also been studied extensively. However, there is one matter common to most such studies. Majority of these methods avoid the complexities involved in a true multi-objective problem and transfrom multi-objectives into a single objective function by using some user defined parameters. Thus most studies in classical multi-objective optimization do not treat multi-objective optimization any differently than single-objective optimization (Figure 1). The studies which are called preference -based approaches,seem to concentrate on various means of converting multiple objectives into a single objective. However, in fact single objective optimization is a degenrate case of multi-objective optimization and multi-objective optimization is not a simple extension of single objective optimization.

Figure1. Schematic of a preferenced-based Multi-Objetive optimization procedure

Although the fundamental difference between these two optimizations lies in the cardinality in the optimal set, from a practical standpoint a user needs only one solution, no matter whether the assocoated optimization problem is single or multi objective. In case of multi-objective optimization user knows a number of solutions with different trade-offs and face with the question of which one to choose. This is not an easy question to answer and involves many other considerations which is usually called Higher Level Information that is non-technical, qualitative and experienced driven. However, if a set of many trade-off solutions are already available, one can evaluate the pros and cons of each of these solutions based on all such non-technical and qualitative, yet still important, considerations and compare them to make a choice. Thus, in a multi-objective optimization, ideally the effort must be made in finding the set of trade-off optimal solutions by considering all objectives to be important. After a set of such trade-off solutions are found, a user can then use higher-level qualitative considerations to make a choice (Figure 2).

Figure 2. Schematic an Ideal Multi-Objective Optimization Procedure

It is mentioned above that the classical way to solve Multi-objective optimization problem is to follow the preference based approach, where a relative preference vector is used to scalarize multiple objectives. Since classical search and optimization methods use a point-by-point approach, where one solution in each iteraion is modified to a different (hopefully better) solution, the outcome of using a classical optimization methos is a single optimized solution. So, the preference based appraoches was motivated by the fact that available optimization methods could find only a single optimized solution in a single simulation run.

However, by introduction of a number of non-classical, stochastic search and optimization algorithms called Evolutionary Algorithms, one deals with a population of solutions in each iteration, instead of a single solution. As a result, the outcome of an EA is also a population of solutions. If an optimization problem has a single optimum, all EA population members can be expected to converge to that optimum solution. However, if an optimization problem has multiple optimal solutions, an EA can be used to capture multiple solutions in its final population. This ability of EA makes it unique in solving Multiple objective optimization problems using the ideal approach.

Early applications to multi-objective optimization problems were mainly preferenced based approaches (e.g. Weighted Sum Method, Weighted Metric Methods, Benson's Method, Value Function Method, Goal Programming Methods, Interactive Methods). The first real application of EAs in finding multiple trade-off solutions in one single simulation run was suggested and worked out in 1984 by David Schaffer. His vector-evaluated genetic algorithm (VEGA) made a simple modification to a single-objective GA to capture multiple trade-off solutions. However, if continued for a large number of iterations, a VEGA population tends to converge to individual optimal solutions. In 1989, David Goldberg, in his seminal book suggested a 10-line sketch of a plausible multi-objective evolutionary algorithm (MOEA) using the concept of domination. Taking the clue from his book, since then a number of different MOEA's have been developed. Of these, Fonesca and Fleming's multi-objective GA (1995), Srinivas and Deb's non-dominated sorting GA (NSGA) (1994), Goldberg's niched Pareto-GA (NPGA) (1994), are among the most poular ones and tested for different real engineering optimization problems.

Principles of Multi-Objective Optimization

Based on the previous disscussion, in the ideal approach for MOOP, it is important to find as many as pareto optimal solutions as possible. Thus, it can be conjectured that there are two goals in a multi-objective optimizatiom:

1. To find a set of solutions as close as possible to the Pareto optimal front.

2. To find a set of solutions as diverese as possible.

For finding the pareto set, most multi-objective optimization algorithms use hte concept of domination. In these algorithms, two solutions are compared on the basis of whether one dominates the other solution or not. A solution x is said to dominate the other solution Y, if both the following conditions are true:

1. The solution X is no worse than Y in all objectives.

2. The solution X is strictly better than Y in at least one objective.

It is intuitive that if a solution X dominates another solution Y, the solution X is better that Y in the parlance of multi-objective optimization. However, if non of X or Y can dominate each other, it is costumary to say that the two solutions are non-dominated with respect to each other. For a given finite set of solutions, we can perform all possible pair-wise comparisions and find which solutions are non-dominated with respect to each other. At the end, we expect to have a set of solutions, any of two which do not dominate each other and for any solution outside this set, we can always find a solution in this set which will dominate the former. In simple term, this means that the solutions of this set are better compared to the rest of solutions which are called the non-dominated set. Thus, the non-dominated set of the entire feasible search space for a multi-objective optimization problem is the Pareto-optimal set for that problem (Figure 3).

Figure 3. Examples of Pareto Optimal sets with Two Objective Functions

Using the concept of domination, one can classify into various non-dominated levels. In most Multi-obejective EAs the population needs to be sorted according to an ascending level of non-domination. The best non-dominated solutions are called the non-dominated set of Level 1. Once the best non-dominated set is identified, they are temporarily disregarded from the population. The non-dominated solutions of the reminaing population are then found and are called non-dominated set of level 2. In order to find the non-dominated set of level 3, all non-dominated set of level 1 and 2 are disregarded and new non-dominated solutions are found. This procedure is continued untill all population members are classified into a non-dominated level.

Based on the non-dominated sorting of the population, one can assign fitness value to the individual solutions. Since, in most EAs, the goal is to maximize all of objective functions, this fitness value can be the number of different fronts we found according to non-dominated sorting minus the corresponding level of that individual. Different methods applied various mappings for fitness calculation but the general idea is the same. Using this concept, EAs can reach to both goals of the multi-objective optimization problem; that is since individuals belonging to a better non-dominated set have a higher fitness value, the algorithm tends to converge to the optimal set (first goal). Moreover, since the individuals in the same front have the same fitness value and there is no mechnism that prefer one over another, the diversity maintains among the set of optimal solutions (second goal). In addition, most EA methods suggest some niche-preserving operator for finding a diverse set of optimal solutions.

Some Existing MOEA Approaches

Based on the method for assigning fitness value and applied niching mechanism there are plenty of MOEA's found in the litreture, some of which are listed below:

1. Vector Evaluated Genetic Algorithm (VEGA), Schaffer, 1984.

2. Vector Optimized Evolution Strategy (VOES), Kursawe, 1990.

3. Weight Based Genetic Algorithm (WBGA), Hajela and Lin, 1993.

4. Random Weighted GA (RWGA), Murata and Ishibuchi, 1995.

5. Multiple Objective Genetic Algorithm (MOGA), Fonesca and Fleming, 1993.

6. Non-Dominated Sorting Genetic Algorithm (NSGA), Srinivas and Deb, 1994.

7. Niched-Pareto Genetic Algorithm (NPGA), Horn et al., 1994.

8. Predator-Prey Evolution Strategy, Laumanns et al., 1998.

9. Rudolph's Elitist Multi-Objective Evolutionary Algorithm, Rudolph, 2001.

10. Elitist non-dominated Sorting Genetic Algorithm (NSGAII), Deb et al., 2000.

11. Distance-Based Pareto Genetic Algorithms (DPGA), Osyczka and Kundu, 1995.

12. Strenght Pareto Evolutionary Algorithm (SPEA), Zitzler and Thiele, 1998.

13. Pareto-Archived Evolution Strategy (PAES), Knowles and Corne, 2000.

14. Multi-Objective Messy Genetic Algorithm, Veldhuizen, 1999.

References

[1] Deb K, Mluti-Objective Optimization using Evolutionary Algorithms, Chichester, UK, Wiley, 2001.

[2] Deb K., Agrawal S., A Fast and Ellitist Multi-Objective Genetic Algorithm: NSGAII, IEEE Transcations on Evolutionary Computaion 6(2) 182-198, 2002.

[3] Knowels D., Corne D., Approximating the non-dominated front using the Pareto archived Evolution Strategy, Evolutionary Computation Journal, 8(2) 149-172-2000.