Non-cooperative game
From DDL Wiki
Game theory can be classified into two discrete areas, cooperative game and non-cooperative game. There are several underlying assumption of game theory that are applicable to both cooperative and non-cooperative games.
- All players are acting rational
- All players can determine their potential outcomes and understand how they can get there
- All players can freely choose to follow a path to get the their most desirable position
In addition to these common attributes, there are some that are specific to cooperative and noncooperative games.
Contents |
Cooperative game
In a cooperative game, the players operate under axiom. Per definition axiom is a proposition that is not susceptible of proof or disproof; its truth is assumed to be self-evident. (Websters Dictionary) That means there are no set external rules, just following a natural order that is accepted as a rule.
Nesling et al. explain that cooperative games are applicable to bargaining, or buyer-seller-negotiations (Nesling, 1983). In contrast to non-cooperative games, the payoff of a participant in a cooperative game is known (Suijs, 1997). Nash explains that in cooperative games, the players are allowed to and will form coalitions that are controlled by an outsider he calls umpire (Nash, 1950).
Noncooperative game
In a noncooperative game on the other hand, all choices are decided by the players based on their own self-interest, presumably without sharing knowledge. Singh describes two formats of those games. In the strategic form the payoff for a given player depends on the strategy of that player and all other participating players. The rules and all available strategies are assumed to be common knowledge. There are no unfair advantages or insider knowledge.
Prisoners Dilemma
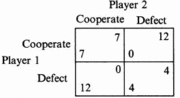
A simple example of this format is the Prisoners Dilemma: Two prisoners (convicted for comitting a crime together) are interrogated separately and have two obvious choices: they can either tell on the other or remain silent. There are different boundary conditions for each choice, as shown in Figure 1.
Depending on what choices are being made, each prisoner faces a sentence of 0, 4, 7 or 12 years. (Andreoni, 1993) The outcomes for each players action based on the other player's action.
Applications
Without going into too much detail, the following section will provide a few examples of applications of (non-cooperative) games.
A market-specific example of a prisoner's dilemma is a Bertrand Game (or Bertrand Duopoly). In this situation, we assume that there are two companies producing exactly the same product. If they both cooperate, they could charge monopoly prices but that means both have the same market share. Each individual player's incentive is to maximize market share, so one drops the price of their product to achieve a higher market share. Both players are now worse off than before.
The Cournot Duopoly on the other hand (in contrast to the Bertrand Duopoly) is a situation, where two firms produce exactly the same product (just like above) but they have to decide how much to produce while the decisions of the other party remain unknown.
Electricity Market
Game theory can be applied to more than just simple examples like the prisoners dilemma or a duopoly. Bompard et al. apply the theory to the energy market and the concept of Market Power. They provide a set of game components specifically for the electricity market, which is a very rigid market with low flexibility and low chances of negotiating (because of fixed distribution infrastructure and supplier locations with respect to customers)
- Game: set of rules that discipline the interactions among competitors
- Payoff: the surplus per producer
- Strategy: decisions on offers that result in maximum payoff
- Move: the payoff achieved as a result of strategy for one player holding the other players' strategies fixed
- Nash Equilibrium: a situation where no producer can improve his situation by changing his strategy (Bompard, 2006)
Singh provides an example for the electricity market. We assume that there are two power generators, both can choose to produce at a high level or a low level. The following table shows the different combinations of outputs (Singh).
Power output of two different power generators:
| Output (MW) | Generator B High | Generator B Low |
|---|---|---|
| Generator A High | A=75, B=75 | A=75, B=20 |
| Generator A Low | A=20, B=75 | A=20, B=20 |
The following table shows the prices that the situations described above will yield.
Prices resulting from the 4 different production scenarios:
| Price ($/MWh) | Generator B High | Generator B Low |
|---|---|---|
| Generator A High | 40 | 45 |
| Generator A Low | 45 | 150 |
The following table illustrates the profits that each producer can expect from the production scenarios given above.
Profits for the production rates:
| Profit ($) | Generator B High | Generator B Low |
|---|---|---|
| Generator A High | A=2250, Profit B=2250 | A=2625, B=700 |
| Generator B Low | A=700, Output B=2625 | A=2800, B=2800 |
We see that the profits show similar tendencies as the Prisoner's Dilemma, see Figure 1. This no market control, the Nash Equilibrium will be in the shaded area (maximized profit at highest price and lowest production) A way to control this situation is to apply contracts for differences (Singh). This allows for a shift in Nash Equilibrium to a more beneficial situation for consumers.
Forecasting
According to Green , the non-cooperative game (unaided judgment) can be applied to forecasting market decisions. This is however, less accurate than using the role playing method and should be used with care (Green, 2005).
Biology
Non-cooperative games (or broader, game theory) has also been applied to biology. The so-called evolution stable strategy is used to describe games that have two different players each one with a specific set of strategies and benefits ("fitness") of that strategy. This theory has been used to explain the relatively constant (equilibrium) female to male ratio of 1:1 (Taylor, 1979).
Marriage
Lundberg et al. apply a bargaining model to marriage. They assume that in each family, there are two decision makers that have an equal decision power and own utility function. The goal of a family is to maximize its well-being, a process which can be modeled by using concepts of both cooperative (as it 'should' be) and also non-cooperative game (as it often is in marriage) (Lundberg, 1996).
See also
References
- Andreoni J, Miller JH, Rational Cooperation in the Finitely Repeated Prisoner's Dilemma: Experimental Evidence, The Economic Journal Vol 103 No. 418 (1993)
- Bompard E, Ma YC, Ragazzi E, Micro-Economic analysis of the physical constrained markets: game theory application to competitive electricity markets, European Physical Journal B, Vol 50 (2006)
- Green KC, Game theory, simulated interaction, and unaided judgement for forecasting decisions in conflicts: Further evidence, International Journal of Forecasting Vol. 21 (2005)
- Lundberg S, Pollak RA, Bargaining and Distribution in Marriage, Journal of Economic Persectives, Vol 10, No. 4 (1996)
- Nash J, Non-Cooperative Games, Annals of Mathematics, Vol. 54, No. 2 (1950)
- Neslin SA, Greenhalgh L, Nash's theory of cooperative games as predictor of the outcomes of buyer-seller negotiations: An experiment in media purchasing, Journal of Marketing Research, Vol. 20, No. 4 (1983)
- Singh H, Introduction to Game Theory and its Application to Electric Power Markets, IEEE Computer Applications in Power
- Suijs J, Borm P, deWaegenaere A, Tijs S, Cooperative games with stochastic payoff, European Journal of Operational Research, Vol. 113 (1999)
- Taylor PD, Evolutionarily Stable Strategies with Two Types of Player, Journal of Applied Probability, Vol. 16, No. 1(1979)